Implementation of Kruskal Algorithm

Hi there! My name is Rishi Vamshi Athinarap, and I am a Master's in computer science student at UNC Charlotte with a passion for Backend Development and DevOps. I believe in the power of learning in public, so I have decided to document my journey and share my learnings with the world through this blog. Whether you're a fellow student looking to learn more about Software Development and DevOps, or a seasoned professional looking to stay up-to-date on the latest trends and technologies, I hope that my insights and experiences can help you grow and succeed in your career. So join me on this journey of continuous learning and discovery, and let's build a brighter future together!

Let's get into the problem statement

A minimum spanning tree (MST) is a way to connect all the vertices in a graph or network with the smallest possible total weight. The vertices in the graph are sometimes called "nodes" and the connections between them are called "edges".

Imagine that you have a map of a city and you want to lay a set of cables to connect all of the buildings in the city with the least amount of cable possible. You could think of each building as a vertex in the graph and the cable connecting the two buildings as an edge. The minimum spanning tree of this graph would be the set of cables that connects all the buildings in the city using the minimum amount of cable.

Many algorithms can be used to find the minimum spanning tree of a graph, such as Kruskal's algorithm and Prim's algorithm. These algorithms work by starting with a subset of the vertices and gradually adding in edges and vertices until the entire graph is connected. They ensure that at each step, the edge added to the tree is the one with the lowest weight so that the total weight of the tree is minimized.

Minimum spanning trees have many practical applications, such as in networking, transportation planning, and image segmentation. They are also used in the study of algorithms and graph theory.

This blog focuses on Kruskal Algorithm - It works by sorting all of the edges in the graph by their weights and adding them to the minimum spanning tree in ascending order.

Here's how the algorithm works:

Sort all the edges in the graph by their weights in ascending order.
Begin with the edge with the smallest weight and add it to the minimum spanning tree.
Check if adding the edge creates a cycle in the minimum spanning tree. If it does, discard the edge. If it doesn't, add it to the minimum spanning tree.
Repeat steps 2 and 3 until all the vertices in the graph are connected.

The key to Kruskal's algorithm is the step where it checks for cycles. When adding an edge to the minimum spanning tree, if the edge connects two vertices that are already in the tree, it will create a cycle. Kruskal's algorithm prevents cycles by only adding edges that do not create them. My implementation to solve this is the following code -

class Kruskal:
    def search(self, parent, i):
        if parent[i] == i:
            return i
        return self.search(parent, parent[i])

    def apply_union(self, parent, rank, x, y):
        xroot = self.search(parent, x)
        yroot = self.search(parent, y)
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot
        else:
            parent[yroot] = xroot
            rank[xroot] += 1

Kruskal's algorithm is used to find the minimum spanning tree because it is guaranteed to find the minimum spanning tree of a graph if one exists. It is also relatively simple to implement and can be used on any type of graph, whether it is connected or not.

The main function to calculate the Minimum spanning tree is -

    def MinimumSpanningTree(self, g_from, g_to, g_weight):
        edges = []
        s = []
        # converting the given inputs to a single edge list
        for i in range(0, len(g_from)):
            s.append(g_from[i] - 1)
            s.append(g_to[i] - 1)
            s.append(g_weight[i])
            edges.append(s)
            s = []

        result = []
        i, e = 0, 0
        # sorting edges list by the last element - which is the weight
        edges = sorted(edges, key=lambda item: item[2])

        parent = g_from + g_to
        parent = list(set(parent))

        for k in range(0, len(parent)):
            parent[k] = parent[k] - 1
        rank = [0] * (len(parent))

        while e < len(parent) - 1:
            u, v, w = edges[i]
            i = i + 1
            x = self.search(parent, u)
            y = self.search(parent, v)
            if x != y:
                e = e + 1
                result.append([u, v, w])
                self.apply_union(parent, rank, x, y)
        for i in range(0, len(result)):
            g_weight.remove(result[i][2])

        # to print the minimum spanning tree
        for u, v, weight in result:
            print("Edge:", u + 1, v + 1, end=" ")
            print("weight -", weight)

        # to calculate the total weight of the minimum spanning tree
        total_weight = 0
        for i in range(0, len(g_weight)):
            if g_weight[i] > 0:
                total_weight = total_weight + g_weight[i]
        return total_weight

Testing the above code based on the following input -

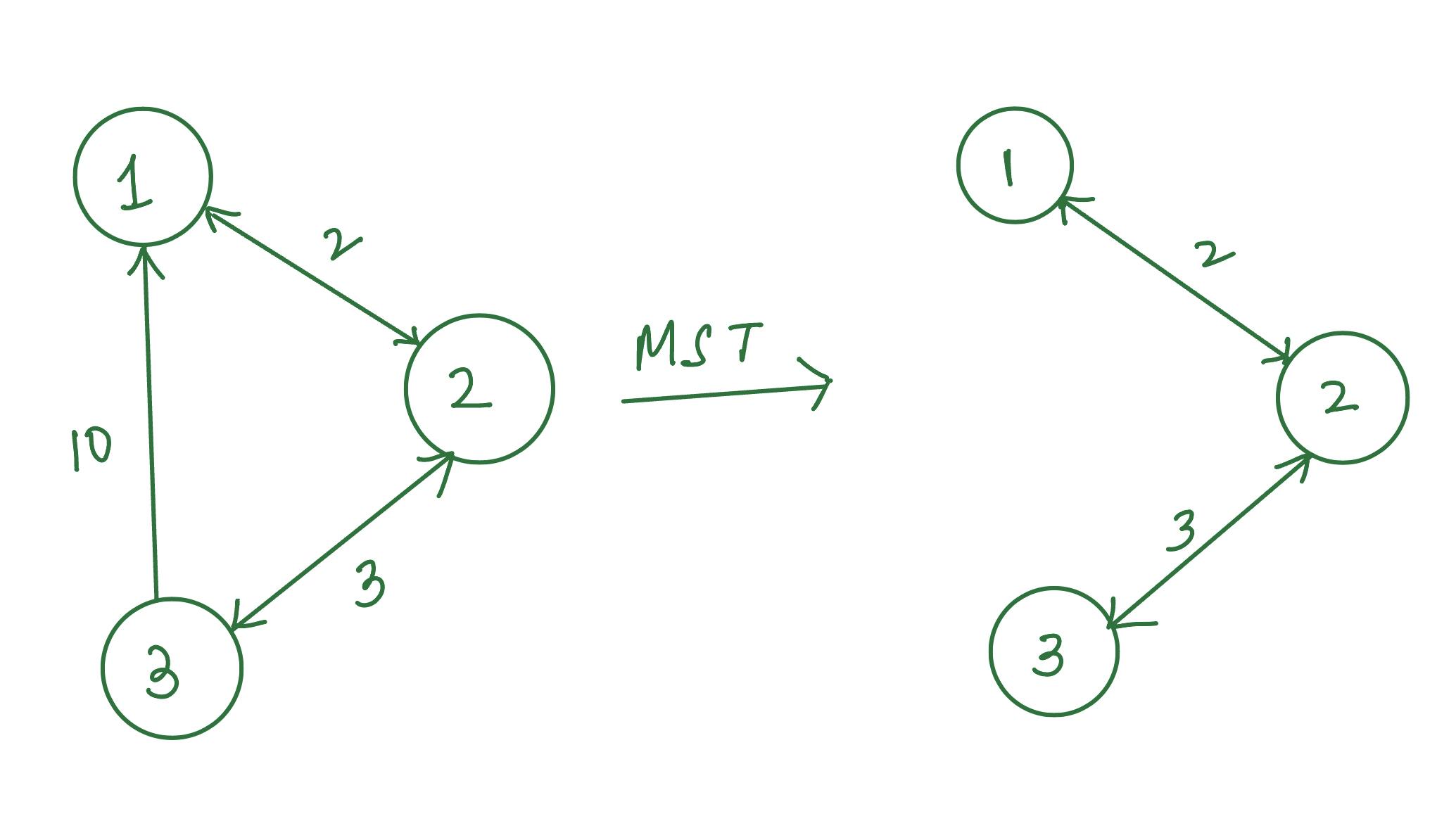
Testing the code -

k = Kruskal()
k.MinimumSpanningTree([1, 2, 2, 3, 3], [2, 1, 3, 1, 2], [2, 2, 3, 10, 3])

Output -

[[0, 1, 2], [1, 0, 2], [1, 2, 3], [2, 0, 10], [2, 1, 3]]
Edge: 1 2 weight- 2
Edge: 2 3 weight- 3

The code for the following code can be found at this link - GitHub

connect with me on linkedin - link

Implementation of Kruskal Algorithm - Part 1

By Rishi Vamshi Athinarap

Let's get into the problem statement